Analyse fondamentale
Équation de Fisher : théorie pour comprendre l’inflation

L'inflation est un phénomène économique complexe qui influence divers aspects de notre vie quotidienne. Elle peut affecter la valeur de notre argent, les taux d'intérêt, et même notre niveau de vie. Mais comment pouvons-nous réellement comprendre et mesurer ses effets sur l'économie ? C'est ce que permet de faire l'équation de Fisher. Dans cet article, nous explorerons les principes fondamentaux de l'équation de Fisher pour mieux comprendre et évaluer les répercussions de l'inflation sur l'économie.

Qu'est-ce que l'équation de Fisher ?
L'équation de Fisher est un outil économique qui relie les taux d'intérêt à l'inflation. Attribuée à l'économiste américain Irving Fisher, elle établit un lien entre le taux d'intérêt nominal, le taux d'intérêt réel et l'inflation anticipée.
L'équation s'exprime ainsi :
| Taux d'intérêt nominal = Taux d'intérêt réel + Taux d'inflation attendu |
| Taux d'intérêt nominal = Taux d'intérêt réel + Taux d'inflation attendu |
Pour calculer le taux d'intérêt réel d'un prêt, il suffit de soustraire le taux d'inflation prévu du taux d'intérêt nominal annoncé.
Par exemple, si les prêteurs exigent un taux d'intérêt réel de 3% et que l'inflation attendue est de 2%, l'équation de Fisher montre que le taux d'intérêt nominal sera de 5%.
Cette équation illustre également l'Effet de Fisher : les augmentations du taux d'inflation entraînent une augmentation équivalente du taux d'intérêt nominal.
Quelle est la différence entre le taux d'intérêt réel et nominal ?
Pour comprendre l'équation de Fisher, il est important de différencier les deux types de taux d'intérêt.
Le taux d'intérêt nominal est le taux affiché qui représente le rendement brut d'une opération. Il ne tient pas compte de l'inflation. En revanche, le taux d'intérêt réel ajuste le rendement pour prendre en compte l'inflation. Il reflète le pouvoir d'achat réel de l'argent. Autrement dit, le taux d'intérêt réel indique combien le rendement augmente réellement après avoir soustrait l'effet de l'inflation.
Ainsi, le taux d'intérêt nominal dans l'équation de Fisher inclut l'inflation, tandis que le taux d'intérêt réel en est déjà dégagé.
👉 Vous pourriez également être intéressé par : Qu’est-ce que l’analyse fondamentale ?
Pourquoi l'équation de Fisher est-elle utile pour expliquer les taux d'intérêt ?
L'équation de Fisher est un outil précieux pour comprendre les taux d'intérêt, car elle montre comment l'inflation et les taux d'intérêt nominaux sont liés. En observant les tendances des taux d’inflation des dernières années, on constate que l'équation de Fisher est souvent respectée.
Lorsque l'inflation augmente, les taux d'intérêt nominaux tendent également à augmenter. À l'inverse, lorsque l'inflation est faible, les taux d'intérêt nominaux sont généralement plus bas.
Cette relation entre les taux d'intérêt et l'inflation est vérifiable dans différents pays. Cela renforce l'importance de l'équation de Fisher pour prédire les taux d'intérêt.
D'ailleurs, les investisseurs en bourse apprécient particulièrement l'équation de Fisher car elle les aide à anticiper les fluctuations des taux d'intérêt. C'est également la raison pour laquelle les entreprises de Wall Street recrutent des experts pour analyser les variations des politiques monétaires et de l'inflation. Ces experts les aident à mieux prédire les taux d'intérêt et à optimiser leurs investissements.
Exemple pour mieux comprendre l'équation de Fisher
Pour mieux comprendre l'équation de Fisher, voyons un exemple. Prenons le cas d'une personne qui demande un prêt. Nous utiliserons une situation peu réaliste pour simplifier l'analyse.
Supposons que Mathias demande un prêt de 1 000 euros. Il achète avec l'argent 1 000 bananes et chaque banane coûte 1 euro. Au moment de l'emprunt, le taux d'intérêt du prêt est de 5%. Ainsi, à la fin de la période, il devra rembourser 1 050 euros, car les intérêts s'élèvent à 50 euros (1 000 * 5%).
Pendant cette même période d'endettement, supposons que l'inflation attendue est de 2%. Par conséquent, les bananes ne coûteront plus 1 euro, mais 1,02 euros chacune.
Que se passe-t-il à la fin de la période de financement ? Si Mathias vend les bananes, il gagnera 1 020 euros (1 000*0,02). C'est-à-dire que le gain serait de 20 euros. Mais en même temps, il a payé des intérêts de 50 euros. Par conséquent, le coût de l'endettement en termes réels est de 30 euros (50-20).
Combien ces 30 euros équivalent-ils en bananes ? Pour le savoir, nous divisons 30 par le prix final de la banane (1,02 euros), ce qui donne un résultat de 29,41 bananes. Ainsi, pour un prêt initial permettant d'acheter 1 000 bananes, il devra rembourser l'équivalent de 29,41 bananes. En d'autres termes, le taux d'intérêt réel est de 2,94 % (29,41/1 000), ce qui est inférieur au taux d'intérêt nominal de 5 %.
Nous pouvons donc constater que l'équation de Fisher est respectée. En effet, le taux d'intérêt nominal de 5% correspond (approximativement) au taux d'intérêt réel (2,94%) plus l'inflation (2%).
Une autre façon d'exprimer l'équation de Fisher
Maintenant, voyons un autre exemple pour expliquer comment l'équation de Fisher peut être analysée d'un autre point de vue. Nous allons présenter la situation d'un prêteur que nous appellerons Victoria. Elle a 12 000 euros qu'elle peut économiser ou prêter.
Si elle prête cet argent, elle accepte un taux d'intérêt annuel de 6%. Alternativement, elle pourrait acheter des chaises et les revendre à un prix plus élevé, en fonction de l'inflation.
Supposons que l'inflation annuelle soit de 4% et que Victoria prête les 12 000 euros à 6% par an. Nous allons calculer le rendement réel du prêt.
Pour simplifier, prenons l'exemple des chaises. Si leur prix initial était de 5 euros, avec une inflation de 4%, le prix final est de 5,2 euros (5 * 1,04).
Le rendement réel est calculé en divisant la valeur finale par l'investissement initial. La valeur finale est le montant prêté plus les intérêts, exprimée en nombre de chaises en utilisant le prix final (5,2 euros). Calculons cela maintenant :
valeur finale = (1+i)/pf
Quel serait alors l'investissement initial ? Pour le déterminer en nombre de chaises, nous devons diviser le montant prêté par le prix du bien au moment de l'investissement, soit 5 euros. Nous appelons ce prix "prix initial" ou "pi".
Comme nous nous intéressons au rendement par euro prêté, nous divisons 1 par le prix initial. Ainsi, l'investissement initial en nombre de chaises est donné par :
Investissement initial = 1 / prix initial (pi)
La formule pour le rendement réel se présente donc comme suit :
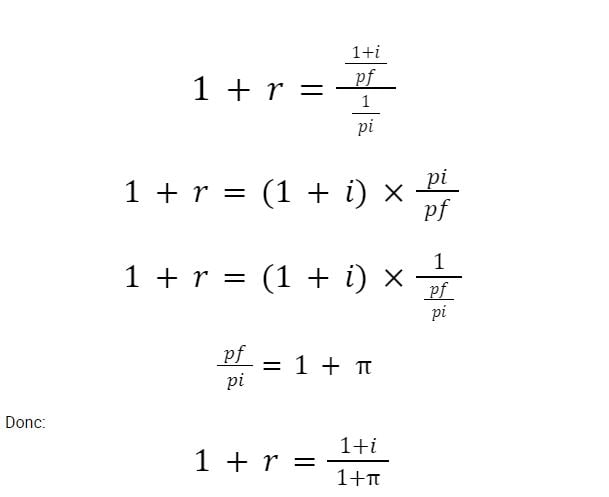
Interprétation du résultat
À l'aide de la formule, nous trouvons que le rendement réel du prêt accordé par Victoria est le suivant :
- 1+r=(1+0,06)/(1+0,04)=1,06/1,04
- 1+r=1,0192
- r=0,0192
- r=1,92%
Cela montre que le rendement réel (1,92 %) est inférieur au taux d'intérêt nominal (6 %). Cette différence est due à l'inflation de 4 %.
De plus, si le taux d'inflation dépasse le taux d'intérêt du prêt, par exemple, à 8 %, le rendement pour Victoria devient négatif :
- 1+r=(1+0,06)/(1+0,08)=1,06/1,08=0,9815
- 1+r=0,9815
- r=-0,0185
- r=-1,85%
Comment expliquer ce résultat ? Victoria aurait mieux fait d'acheter des chaises et de les revendre à un prix plus élevé plutôt que d'accorder le prêt.
Au lieu de voir le prix des chaises passer de 5 à 5,2 euros, il a augmenté à 5,4 euros. Avec les 12 000 euros, Victoria aurait acheté 2 400 chaises (12 000 / 5). En les revendant à 5,4 euros chacune, elle aurait obtenu 12 960 euros (2 400 * 5,4), soit un gain de 960 euros (12 960 - 12 000). En revanche, en accordant le prêt, elle n'aurait gagné que 720 euros (12 000 * 0,06).
Cet exemple montre que si Victoria anticipe une inflation plus élevée, elle exigera également un taux d'intérêt nominal plus élevé pour éviter un rendement négatif. Cela illustre clairement la relation entre les trois variables dans l'équation de Fisher.