Bourse
Coût marginal : définition et utilité

Le coût marginal représente la variation constatée dans le coût total de production avec l'ajout d'une unité. Ce principe trouve une large application en microéconomie.
Ce concept illustre le coût engendré par la production d'une unité additionnelle d'un bien ou service. Sa compréhension est cruciale car elle nous informe sur le prix minimal de vente acceptable pour notre produit.
Pour réaliser un profit, le prix de vente doit excéder le coût marginal. Prenons un exemple : le coût marginal pour produire une barre de chocolat s'élève à 0,50 €. Pour en tirer profit, il faut la vendre à un prix supérieur à 0,50 €.
Dans l'éventualité où le prix de marché est inférieur au coût marginal, l'entreprise subira des pertes sur chaque unité vendue. À l'inverse, si le prix de marché dépasse le coût marginal, l'entreprise bénéficiera de profits.
Coût marginal et coût moyen
L'impact du coût marginal sur le coût moyen mérite d'y prêter attention. S'il reste inférieur au coût moyen, alors augmenter la production diminue ce dernier. En revanche, si il dépasse le coût moyen, et que la production s'élargit, le coût moyen s'accroît.
Il est essentiel de se remémorer que le coût moyen résulte de la division du coût total par le volume total produit.
Pour illustrer cette dynamique, considérons l'obtention de 40 unités pour un coût total de 800 €. Le coût moyen atteint ainsi 20 € (soit 800/40). Si produire l'unité 41 coûte 21 €, le coût total s'élève à 821 € (800 plus 21). Le coût moyen s'ajuste donc à 20,0244 € (821 divisé par 41).
Coût marginal Formule
En termes de mathématiques, on calcule le coût marginal en prenant la dérivée de la fonction de coût total (CT) en fonction d'une quantité donnée (Q).
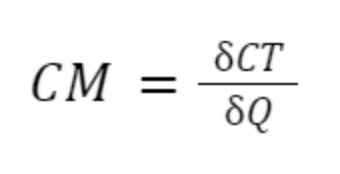
Ainsi, cet indicateur reflète l'accroissement du coût total résultant d'une unité supplémentaire produite.
La courbe du coût marginal
La courbe du coût marginal illustre comment le ce dernier évolue avec la quantité produite. Elle se trace sur un graphique, l'axe horizontal (X) représentant la quantité et l'axe vertical (Y) le coût marginal. Typiquement, cette courbe adopte une forme en U. Cette configuration découle de la loi des rendements décroissants. Autrement dit, l'accroissement de la production d'un facteur, les autres restant constants, engendre un rendement décroissant.
Prenons l'exemple d'une fabrique de crayons pour clarifier ce concept. Avec l'équipement actuel, la production optimale peut atteindre 10.000 crayons par semaine. Au-delà de ce seuil, seuls les coûts variables comme la main-d'œuvre et les matières premières (ex. le graphite) augmentent en fonction de la production désirée.
Pour augmenter la production au-delà de 10.000 unités par semaine, l'ajout de travailleurs n'est plus efficace. En effet, ils entraveraient mutuellement leur travail. De même, la capacité actuelle de la machinerie limite le traitement des matières premières. Plus de temps serait nécessaire pour cela. À ce stade, le coût marginal arrête de diminuer et commence à augmenter. Pour accroître la production de crayons efficacement, l'entreprise doit agrandir sa capacité, ce qui augmente les coûts fixes.
Il est important de noter que chaque processus de production présente des caractéristiques uniques. Dans certains cas, les coûts fixes peuvent être relativement faibles, tandis que dans d'autres, ils représentent une part plus importante du coût total de production.
Le graphique ci-dessous illustre un point crucial : le moment où le coût marginal rencontre le revenu marginal. À ce point, le revenu marginal s'aligne sur le prix. Cela décrit la courbe de la relation entre le revenu et le coût par unité produite.
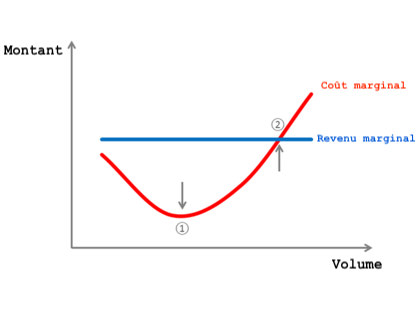
Exemple de coût marginal
Considérons un exemple concret. Imaginons que pour produire 400 unités d'un produit, nous disposons des informations suivantes.
- Coûts fixes : 3.000 €
- Coûts variables : 500 €
- De plus, nous savons que l'unité 401 ne nécessite pas plus de coûts fixes, mais les coûts variables doivent être augmentés à 520 €.
Demandons-nous alors quel est le coût marginal de cette 401e unité.
coût total de l'unité 40 : 3.000+500= 3.500 €
coût total de l'unité 41 : 3.000+520= 3.520 €
coût marginal : 3.520-3.500= 520-500=20 €
coût moyen : 3.520/41= 85,8537 €
Concepts liés :
Voici quelques concepts liés :
- Coûts fixes : Ce sont des dépenses qui ne varient pas. Elles restent constantes, indépendamment du volume de production. Un exemple pertinent est le loyer d'une installation industrielle, qui représente un coût fixe.
- Coûts variables : Ces coûts fluctuent en fonction de la production. Ils varient directement avec le nombre d'unités produites. Le coût des matériaux nécessaires à la fabrication en est un exemple, qualifié de coût variable.
- Coûts totaux : Cette valeur représente l'addition des coûts fixes et variables. Elle constitue la dépense globale engagée.
- Coût moyen ou unitaire : Il s'agit du coût par unité produite. Pour le déterminer, on divise les coûts totaux par le volume d'unités produites. Cela donne le coût moyen d'un bien ou d'un service.
👉 N'hésitez à consulter nos autres articles sur les indicateurs économiques ou financiers :