Calculatrice d’intérêts composés

Transformez vos investissements et atteignez vos objectifs financiers avec le pouvoir de l'intérêt composé. Notre calculatrice d'intérêts composés simplifie la planification de vos investissements, vous permettant de visualiser la croissance de votre patrimoine et d'optimiser vos rendements.

Découvrez comment de petits apports réguliers peuvent se multiplier au fil du temps, et peuvent vous aider à atteindre vos objectifs financiers, assurer votre retraite, payer l'éducation de vos enfants ou simplement acquérir des biens.

Calculatrice d'intérêts composés : un outil essentiel

Notre calculatrice d'intérêts composés est un outil indispensable pour la planification financière et les investissements. Elle permet d'estimer la valeur future d'un investissement en tenant compte de différents taux d'intérêt, périodes de temps et contributions régulières.

Essayez différents scénarios et voyez comment de simples ajustements peuvent avoir un impact significatif sur la croissance de votre investissement.

👉 Pour plus d'informations : Taux d’intérêt et bourse : impact sur vos investissements

Comment utiliser la calculatrice d'intérêts composés

Mode d'utilisation :

• Investissement initial : c'est le montant d'argent que vous allez investir au départ.
• Taux d'intérêt : le taux que vous espérez gagner sur votre investissement.
• Investissement additionnel : le montant que vous prévoyez d'ajouter et la fréquence.
• Durée : c'est le temps en années que durera l'investissement.
• Les intérêts sont composés : la fréquence à laquelle les intérêts sont calculés sur votre investissement.

Qu'est-ce que l'intérêt composé ?

Les intérêts composés sont donnés par l'accumulation d'intérêts générés sur une certaine période à partir d'un capital à un taux d'intérêt, pendant certaines périodes d'application. Cela signifie qu'à la fin de chaque période, un montant plus important est obtenu pour la nouvelle période en utilisant le même taux d'intérêt.

Caractéristiques de l'intérêt composé

La principale caractéristique des intérêts composés, et ce qui les distingue des intérêts simples, est que ce modèle financier permet la réinvestissement du capital plus les intérêts à chaque période d'exercice.

En capitalisant l'investissement, le capital réinvesti à chaque période est plus grand, ce qui augmente progressivement le montant des intérêts obtenus. C'est une sorte de boule de neige descendante qui permet d'obtenir une plus grande rentabilité au fil du temps, en utilisant le même capital initial.

Cependant, une autre caractéristique des produits d'investissement à intérêts composés est qu'il n'est pas possible de disposer des intérêts générés par le capital jusqu'à ce que la période établie soit terminée.

Contrairement aux intérêts simples, où l'on peut retirer les gains et réinvestir le même capital, dans les intérêts composés, la clé est précisément que les intérêts générés à chaque période servent à augmenter le capital initial. Si un retrait de n'importe quel montant d'argent est effectué, cela résulterait en la non-conformité avec la formule des intérêts composés.

Formule des intérêts composés

Les intérêts composés sont calculés comme le montre la formule ci-dessous. Nous n'aurons besoin que de quelques données : le capital initial, les intérêts et la durée de l'investissement. La première étape est de comprendre les variables de ce calcul :

VA=VF (1 + i)^n

• VF = c'est la valeur initiale de l'opération, c'est-à-dire le montant que vous avez investi ;
• VA = la valeur que vous recevrez à la fin de la période, c'est-à-dire la valeur initiale + intérêts ;
• i = taux d'intérêt, c'est-à-dire le facteur qui sera utilisé pour multiplier le capital.
• n = c'est la période pendant laquelle le taux sera appliqué sur la valeur initiale.

Exemple de calcul d'intérêts composés

Nous donnons un exemple de comment calculer les investissements et ensuite nous expliquerons les chiffres:

Marc investit un capital initial de 5.000 euros dans un produit financier à intérêt simple qui génère un taux d'intérêt de 2% pendant un an. À la fin du mandat, Marc obtient son capital initial plus l'intérêt simple généré pendant cette période, c'est-à-dire, 5.100 euros.

Maintenant, supposons que Marc utilise ces mêmes 5.000 euros plus le profit de cette première année (100 euros) pour commencer à générer des intérêts composés, au même taux de 2% ; à la fin de la période (que nous estimons à 12 ans) le profit total de l'investissement serait de 6.341,21 euros.

Comme nous pouvons le voir, le taux d'intérêt ne change à aucun moment. Il est de 2% chaque année et applique des intérêts composés sur le capital à chaque période. De cette manière, les intérêts s'ajoutent d'année en année et l'on gagne un peu plus chaque année. En résumé : plus le capital est grand, plus l'intérêt généré est grand, il est ensuite accumulé au capital, qui à son tour est réinvesti, résultant en un total bien supérieur à ce qui serait obtenu avec un intérêt simple.

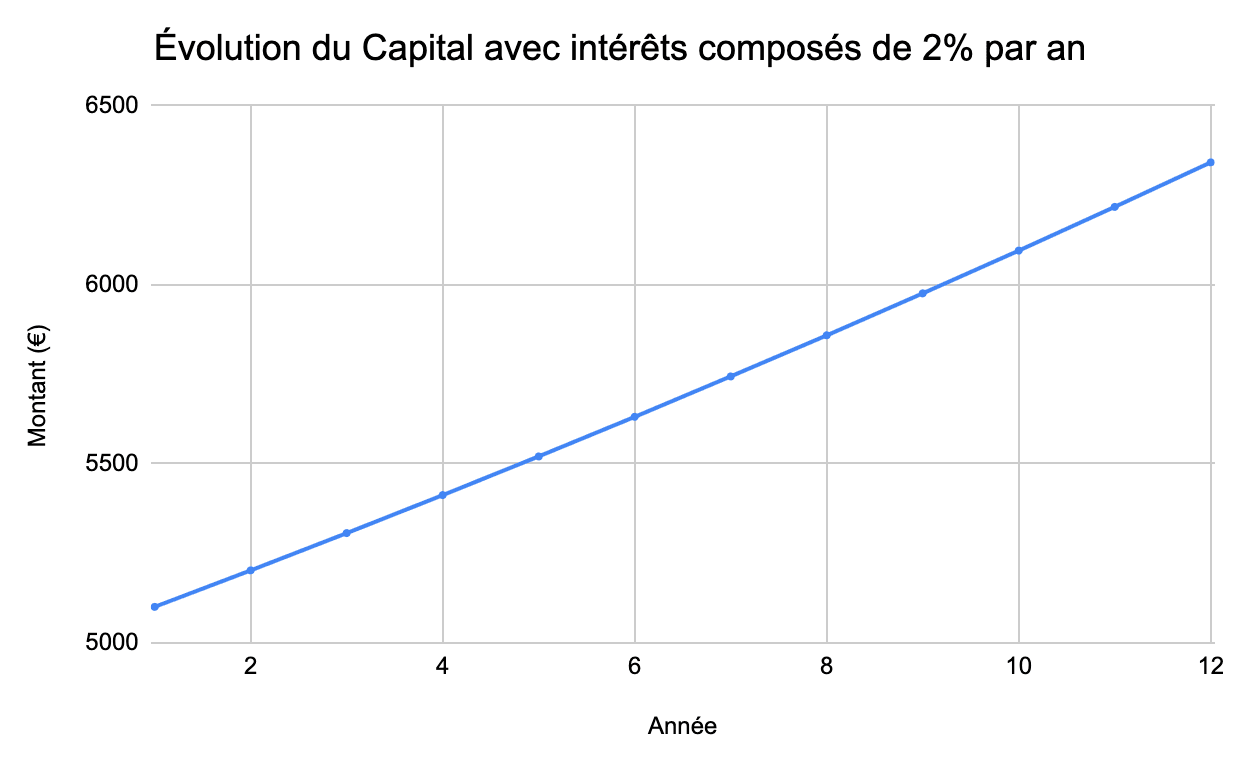
Pour mieux comprendre ce concept, n'hésitez pas à essayer vous-même avec notre calculatrice d'intérêts composés.

Quelle est la différence entre les intérêts simples et composés ?

Dans le régime des intérêts simples, le pourcentage d'intérêt ne s'applique qu'au capital initial. Cela signifie que la rémunération sur l'argent n'aura d'incidence que sur le montant investi ou prêté initialement.

Les principales différences entre les intérêts simples et composés sont les suivantes:

Intérêts simples

Voici les caractéristiques des intérêts simples qui se démarquent :

• Le capital initial ne change pas, il reste le même tout au long de l'opération.
• L'intérêt ne change pas, il est le même pour chaque période de l'opération.
• Le taux d'intérêt est appliqué sur le capital investi ou sur le capital initial.

Intérêts composés

Les principales caractéristiques des intérêts composés sont :

• Le capital initial augmente à chaque période à mesure que les intérêts augmentent.
• Le taux d'intérêt est appliqué sur le capital qui va varier
• L'intérêt va augmenter.

Quel que soit le montant initial - que ce soit 1.000, 5.000, 20.000 ou 100.000 euros, le secret pour atteindre une croissance significative du patrimoine réside dans l'application intelligente des intérêts composés. Voici un guide concis pour ajuster vos stratégies d'investissement en fonction du capital disponible, dans le but de maximiser le rendement à long terme :

• Pour les investisseurs débutants : Avec seulement 1 000 euros, explorez des options d'investissement à faible coût et à fort potentiel de croissance, comme les ETF et les fonds d'investissement. Un début précoce est essentiel pour tirer le meilleur parti des intérêts composés. En savoir plus sur comment bien investir 1000 euros.
• Passer au niveau supérieur : En investissant 5 000 euros, envisagez de diversifier avec des actions individuelles, des ETF thématiques et des obligations, en cherchant un équilibre entre risque et rendement.
• Élargir les horizons : Avec un montant de 20 000 euros, la diversification devient cruciale. Combinez des classes d'actifs comme l'immobilier et les cryptomonnaies avec des investissements traditionnels pour minimiser les risques et maximiser les rendements.
• Décisions importantes pour de grands montants : Si vous pensez investir 100 000 euros ou plus, il est recommandé de chercher des conseillers financiers pour personnaliser votre stratégie d'investissement, en se concentrant sur des fonds à haute performance et des opportunités exclusives qui maximisent les avantages des intérêts composés.

Courtiers qui font croître votre argent

Dans l'univers de la finance, le choix d'un courtier qui valorise et rémunère le capital déposé est un avantage significatif. Des courtiers comme Interactive Brokers, Freedom 24 et XTB transcendent l'offre traditionnelle en appliquant des intérêts composés sur les soldes non investis, assurant que votre argent ne repose pas seulement, mais croît. Ce modèle de rémunération témoigne d'un engagement envers la valorisation des ressources des investisseurs, favorisant une accumulation de richesse plus efficace et durable.

Cet article est purement informatif et éducatif. Les informations fournies ici ne peuvent pas être considérées comme des conseils financiers ou des recommandations d'achat / vente

FAQ sur les Intérêts Composés