Bourse
La covariance : définition et formule
La covariance mesure la relation entre deux variables aléatoires. Lorsque ces variables ne présentent aucun lien, la covariance affiche zéro.
Elle cherche à déterminer dans quelle mesure les deux variables évoluent ensemble. Elles peuvent évoluer soit dans la même direction, soit dans des directions contraires.
Formule de la covariance
La formule de la covariance s'applique en prenant deux variables, nommées x et y. On utilise alors l'équation suivante :
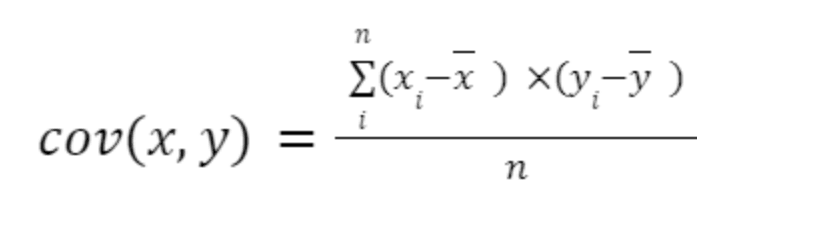
Ici, x et y, surmontés d'une barre horizontale, symbolisent la moyenne des données. De plus, n représente le total des observations.
Dans le cas d'un tableau de fréquences avec des données groupées, la formule se modifie comme suit :
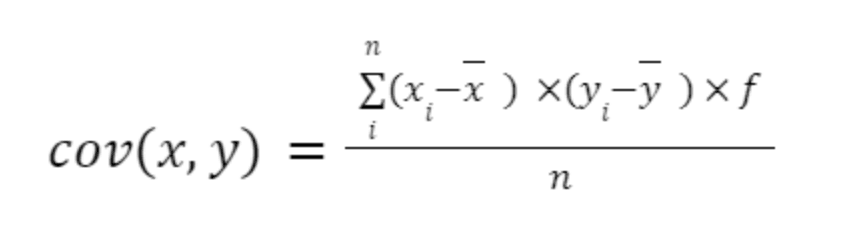
Ici, f désigne la fréquence, ou le nombre de répétitions de chaque observation, pour x ainsi que pour y. Cela se précisera à travers un exemple ultérieur.
Propriétés de la covariance
Les caractéristiques essentielles de la covariance incluent :
- La covariance entre une variable et une constante est toujours nulle.
- La covariance entre une variable et elle-même équivaut à la variance de ladite variable.
- Lorsque la covariance se révèle positive, les deux variables tendent à évoluer de concert. En effet, une augmentation de x entraîne une hausse de y. À l'inverse, une covariance négative signale une relation inverse entre les variables. Ainsi, si l'une augmente, l'autre diminue, et réciproquement.
- Une covariance nulle indique l'absence de lien discernable entre les variables concernées.
- Modifier l'unité de mesure des variables, par exemple passer de grammes à kilogrammes, modifie le résultat de la covariance. Il est important de souligner que la covariance n'est pas une mesure normalisée. Cela complique la comparaison des covariances entre elles.
Applications de la covariance
Certaines des principales applications de la covariance dans la prise de décisions d'investissement sont :
- Mesurer le risque : Elle permet de mesurer le risque d'un investissement dans un actif ou un portefeuille d'actifs. Une haute covariance indique un risque élevé, tandis qu'une faible covariance indique un faible risque.
- Évaluer la diversification : La covariance permet également d'évaluer la diversification d'un portefeuille d'actifs. Un portefeuille hautement diversifié aura une faible covariance, ce qui indique un faible risque. Par conséquent, la covariance peut aider les investisseurs à sélectionner des actifs qui se complètent entre eux et à réduire le risque du portefeuille.
- Déterminer le rendement attendu : La covariance est également utilisée pour déterminer le rendement attendu d'un portefeuille d'actifs. Le rendement attendu est calculé comme le produit de la covariance entre le rendement de chaque actif et son poids dans le portefeuille. Cette information peut aider les investisseurs à prendre des décisions sur quels actifs inclure dans leur portefeuille et dans quelle proportion.
Différences et complémentarités avec la corrélation
La covariance et la corrélation constituent deux notions essentielles. Elles se rapportent au risque et à la diversification dans le domaine de l'investissement. Pourtant, elles présentent certaines distinctions notables.
La covariance mesure l'interdépendance entre deux variables. En revanche, la corrélation offre une évaluation normalisée de cette même interdépendance. Pour calculer la covariance, on multiplie les écarts des valeurs de chaque variable par rapport à leur moyenne. Ensuite, on divise le total par le nombre d'observations. Ce procédé éclaire sur la manière dont les variables évoluent conjointement. Toutefois, il ne révèle pas l'intensité de leur lien.
D'autre part, la corrélation se détermine en divisant la covariance par le produit des écarts-types des deux variables. Cette méthode produit une mesure standardisée de l'interaction entre les variables. Elle facilite la comparaison de l'intensité de leurs relations respectives. La corrélation se traduit par un chiffre compris entre -1 et 1. Un chiffre de 1 signale une corrélation totalement positive. Un score de -1, quant à lui, indique une corrélation parfaitement négative. Un résultat nul signifie l'absence de corrélation entre les variables.
Applications pratiques du calcul de la covariance
Par exemple, mesurons le poids et la taille d'une personne à des intervalles fixes. Ceci tout au long de sa vie. Ainsi, on peut calculer la covariance entre le poids et la taille. Ce calcul se fait à chaque moment. Cela fournit une mesure de la corrélation étroite entre le poids et la taille. La mesure s'étend au fil du temps. Si le poids et la taille étaient parfaitement corrélés, la covariance atteindrait 1. Dans le cas contraire, où aucune corrélation n'existerait, elle serait 0.
Dans le domaine de l'investissement, un exemple est également pertinent. Si vous souhaitez évaluer la santé du marché boursier, regardez le Dow Jones Industrial Average (DJIA) et le S&P 500. Le DJIA reflète l'évolution des prix des actions de 30 grandes entreprises. Parallèlement, le S&P 500 suit celle de 500 grandes entreprises. Pour juger de la santé du marché boursier, nous calculerions la covariance entre ces deux indices. Ce calcul indiquerait le degré de mouvement relatif de chaque ensemble de données par rapport à l'autre.
Exemples d'utilisation
Supposons que nous avons deux variables, x et y, avec 32 observations de chacune
| X | Y | ||||
| 1 | 10 | 5 | |||
| 2 | 5 | 10 | |||
| 3 | 3 | 3 | |||
| 4 | 10 | 8 | |||
| 5 | 10 | 9 | |||
| 6 | 8 | 1 | |||
| 7 | 8 | 8 | |||
| 8 | 5 | 1 | |||
| 9 | 1 | 2 | |||
| 10 | 8 | 4 | |||
| 11 | 9 | 1 | |||
| 12 | 4 | 7 | |||
| 13 | 8 | 5 | |||
| 14 | 8 | 7 | |||
| 15 | 6 | 4 | |||
| 16 | 3 | 4 | |||
| 17 | 5 | 8 | |||
| 18 | 4 | 2 | |||
| 19 | 10 | 1 | |||
| 20 | 2 | 1 | |||
| 21 | 1 | 6 | |||
| 22 | 3 | 8 | |||
| 23 | 8 | 9 | |||
| 24 | 3 | 1 | |||
| 25 | 3 | 10 | |||
| 26 | 8 | 7 | |||
| 27 | 5 | 3 | |||
| 28 | 9 | 1 | |||
| 29 | 7 | 5 | |||
| 30 | 5 | 4 | |||
| 31 | 9 | 6 | |||
| 32 | 8 | 8 | |||
| prom | 6,1250 | 4,9688 |
| X | Y | |
| 1 | 10 | 5 |
| 2 | 5 | 10 |
| 3 | 3 | 3 |
| 4 | 10 | 8 |
| 5 | 10 | 9 |
| 6 | 8 | 1 |
| 7 | 8 | 8 |
| 8 | 5 | 1 |
| 9 | 1 | 2 |
| 10 | 8 | 4 |
| 11 | 9 | 1 |
| 12 | 4 | 7 |
| 13 | 8 | 5 |
| 14 | 8 | 7 |
| 15 | 6 | 4 |
| 16 | 3 | 4 |
| 17 | 5 | 8 |
| 18 | 4 | 2 |
| 19 | 10 | 1 |
| 20 | 2 | 1 |
| 21 | 1 | 6 |
| 22 | 3 | 8 |
| 23 | 8 | 9 |
| 24 | 3 | 1 |
| 25 | 3 | 10 |
| 26 | 8 | 7 |
| 27 | 5 | 3 |
| 28 | 9 | 1 |
| 29 | 7 | 5 |
| 30 | 5 | 4 |
| 31 | 9 | 6 |
| 32 | 8 | 8 |
| prom | 6,1250 | 4,9688 |
À la fin du tableau, nous avons d'abord calculé les moyennes. Ensuite, nous avons appliqué la formule de la covariance indiquée précédemment. Nous procéderons par étapes.
Étape suivante : normalisation des données
Par conséquent, nous soustrayons chaque observation de la moyenne de la variable (x et y en gras). Ensuite, nous multiplions les résultats obtenus.
| xi-x | yi-y | (xi-x)*(yi-y) | |||
| 3,8750 | 0,0313 | 0,1211 | |||
| -1,1250 | 5,0313 | -5,6602 | |||
| -3,1250 | -1,9688 | 6,1523 | |||
| 3,8750 | 3,0313 | 11,7461 | |||
| 3,8750 | 4,0313 | 15,6211 | |||
| 1,8750 | -3,9688 | -7,4414 | |||
| 1,8750 | 3,0313 | 5,6836 | |||
| -1,1250 | -3,9688 | 4,4648 | |||
| -5,1250 | -2,9688 | 15,2148 | |||
| 1,8750 | -0,9688 | -1,8164 | |||
| 2,8750 | -3,9688 | -11,4102 | |||
| -2,1250 | 2,0313 | -4,3164 | |||
| 1,8750 | 0,0313 | 0,0586 | |||
| 1,8750 | 2,0313 | 3,8086 | |||
| -0,1250 | -0,9688 | 0,1211 | |||
| -3,1250 | -0,9688 | 3,0273 | |||
| -1,1250 | 3,0313 | -3,4102 | |||
| -2,1250 | -2,9688 | 6,3086 | |||
| 3,8750 | -3,9688 | -15,3789 | |||
| -4,1250 | -3,9688 | 16,3711 | |||
| -5,1250 | 1,0313 | -5,2852 | |||
| -3,1250 | 3,0313 | -9,4727 | |||
| 1,8750 | 4,0313 | 7,5586 | |||
| -3,1250 | -3,9688 | 12,4023 | |||
| -3,1250 | 5,0313 | -15,7227 | |||
| 1,8750 | 2,0313 | 3,8086 | |||
| -1,1250 | -1,9688 | 2,2148 | |||
| 2,8750 | -3,9688 | -11,4102 | |||
| 0,8750 | 0,0313 | 0,0273 | |||
| -1,1250 | -0,9688 | 1,0898 | |||
| 2,8750 | 1,0313 | 2,9648 | |||
| 1,8750 | 3,0313 | 5,6836 |
| xi-x | yi-y | (xi-x)*(yi-y) |
| 3,8750 | 0,0313 | 0,1211 |
| -1,1250 | 5,0313 | -5,6602 |
| -3,1250 | -1,9688 | 6,1523 |
| 3,8750 | 3,0313 | 11,7461 |
| 3,8750 | 4,0313 | 15,6211 |
| 1,8750 | -3,9688 | -7,4414 |
| 1,8750 | 3,0313 | 5,6836 |
| -1,1250 | -3,9688 | 4,4648 |
| -5,1250 | -2,9688 | 15,2148 |
| 1,8750 | -0,9688 | -1,8164 |
| 2,8750 | -3,9688 | -11,4102 |
| -2,1250 | 2,0313 | -4,3164 |
| 1,8750 | 0,0313 | 0,0586 |
| 1,8750 | 2,0313 | 3,8086 |
| -0,1250 | -0,9688 | 0,1211 |
| -3,1250 | -0,9688 | 3,0273 |
| -1,1250 | 3,0313 | -3,4102 |
| -2,1250 | -2,9688 | 6,3086 |
| 3,8750 | -3,9688 | -15,3789 |
| -4,1250 | -3,9688 | 16,3711 |
| -5,1250 | 1,0313 | -5,2852 |
| -3,1250 | 3,0313 | -9,4727 |
| 1,8750 | 4,0313 | 7,5586 |
| -3,1250 | -3,9688 | 12,4023 |
| -3,1250 | 5,0313 | -15,7227 |
| 1,8750 | 2,0313 | 3,8086 |
| -1,1250 | -1,9688 | 2,2148 |
| 2,8750 | -3,9688 | -11,4102 |
| 0,8750 | 0,0313 | 0,0273 |
| -1,1250 | -0,9688 | 1,0898 |
| 2,8750 | 1,0313 | 2,9648 |
| 1,8750 | 3,0313 | 5,6836 |
La somme de la troisième colonne, celle située tout à droite, atteint 33,125. Nous la divisons ensuite par le nombre total de données, 32. Ainsi, nous obtenons 1,0352 comme résultat.
Or, vu qu'il y a 32 données, nous pourrions envisager un échantillon. Ainsi, la division ne se fait pas par n, mais par n-1. Le nouveau résultat est 1,0685 (33,125/31).
Il est crucial de mentionner qu'il est possible de calculer la formule de la covariance avec Excel et d'autres logiciel qui incluent déjà une fonction. Elle est utilisable tant pour une population que pour un échantillon. Il devient donc inutile de réaliser ce calcul à la main.
Covariance sur des données groupées
Observons maintenant un exemple très simplifié. Il illustre comment calculer la covariance pour des données groupées. Dans cet exemple, f représente la fréquence de répétition du même résultat. Ceci est valable tant pour x que pour y.
Nous commencerons par examiner les données non groupées :
| x | y | ||
| 3 | 6 | ||
| 4 | 7 | ||
| 3 | 6 | ||
| 3 | 6 | ||
| 4 | 7 | ||
| 5 | 9 | ||
| 4 | 7 | ||
| 5 | 9 | ||
| 2 | 5 | ||
| 6 | 9 |
| x | y |
| 3 | 6 |
| 4 | 7 |
| 3 | 6 |
| 3 | 6 |
| 4 | 7 |
| 5 | 9 |
| 4 | 7 |
| 5 | 9 |
| 2 | 5 |
| 6 | 9 |
Maintenant, regroupés :
| x | y | f | |||
| 3 | 6 | 3 | |||
| 4 | 7 | 3 | |||
| 5 | 9 | 2 | |||
| 2 | 5 | 1 | |||
| 6 | 9 | 1 |
| x | y | f |
| 3 | 6 | 3 |
| 4 | 7 | 3 |
| 5 | 9 | 2 |
| 2 | 5 | 1 |
| 6 | 9 | 1 |
| (xi-x) | (yi-y) | (xi-x)*(yi-y)*f | |||
| -0,90 | -1,10 | 2,97 | |||
| 0,10 | -0,10 | -0,03 | |||
| 1,10 | 1,90 | 4,18 | |||
| -1,90 | -2,10 | 3,99 | |||
| 2,10 | 1,90 | 3,99 |
| (xi-x) | (yi-y) | (xi-x)*(yi-y)*f |
| -0,90 | -1,10 | 2,97 |
| 0,10 | -0,10 | -0,03 |
| 1,10 | 1,90 | 4,18 |
| -1,90 | -2,10 | 3,99 |
| 2,10 | 1,90 | 3,99 |
Nous avons mis au point une méthode semblable à celle décrite dans l'exemple antérieur (x et y représentent ici les moyennes arithmétiques des variables concernées).
La somme figurant dans la troisième colonne du tableau mentionné atteint 15,10. Nous la divisons par (n-1), partant du principe que nous travaillons sur un échantillon. Cela nous donne 1,6778 (soit 15,10 divisé par 9).