Analyse technique
Comment utiliser les moyennes mobiles ?
Les moyennes mobiles constituent une moyenne du prix d'un actif pendant un certain nombre de périodes. La caractéristique mobile implique que la moyenne prend en compte les nouvelles données et écarte les données les plus anciennes.
La moyenne mobile est un bon indicateur de tendances. Dans l'analyse boursière, 3 moyennes mobiles sont les plus utilisées : moyenne mobile simple, moyenne mobile exponentielle ou EMA et moyenne mobile pondérée. (Nous expliquerons plus tard la différence entre elles avec un exemple).
Moyennes Mobiles: qu'est-ce que c'est ?
Les moyennes mobiles sont utilisées pour la détection des tendances, des supports et des résistances. Ils nous offrent également des signaux d'entrée et de sortie lorsque le prix coupe la moyenne mobile.
On combine généralement des moyennes mobiles de différents espaces temporels :
- À court terme : entre 3 et 25 périodes
- À moyen terme : entre 30 et 75 périodes
- À long terme : entre 100 et 250 périodes.
Parmi les moyennes mobiles les plus importantes, nous trouvons la moyenne mobile de 50 et de 200 séances comme référence pour la plupart des investisseurs.
Par défaut, les moyennes mobiles sont calculées sur le prix de clôture, bien que certaines stratégies puissent également se baser sur le calcul des moyennes mobiles sur le prix d'ouverture, le maximum ou le minimum de la période sélectionnée (jour, heure, minute...).
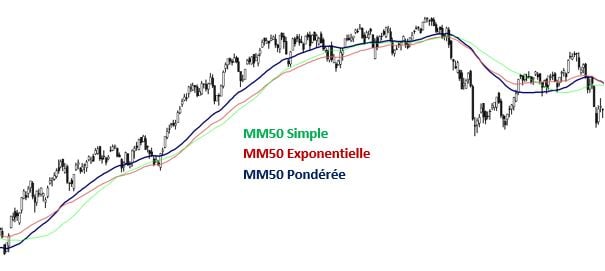
Sur le graphique, nous voyons une comparaison de la moyenne mobile de 50 périodes, mais avec 3 approximations différentes, et la pondérée est celle qui s'ajuste le mieux au prix, étant la simple celle qui s'éloigne le plus lorsque le prix subit des variations.
Moyenne mobile simple
La moyenne mobile simple additionne le prix d'un nombre de périodes déterminées et le divise par le nombre de périodes choisi, de sorte qu'elle calcule la moyenne.

Une moyenne mobile simple de 20 jours additionne le prix (de clôture) d'un actif pendant les 20 derniers jours et le résultat est divisé par 20. Cette opération est mise à jour avec les nouvelles données entrantes, en écartant les données anciennes, de sorte que nous obtiendrons toujours la moyenne mobile simple des 20 dernières séances.
Moyenne mobile exponentielle
La moyenne mobile exponentielle cherche à donner plus d'importance aux cotations les plus récentes en utilisant un pondérage ou un lissage exponentiel. Le facteur de lissage est 2/(Periodo+1). De cette façon, on parvient à lisser la série de prix, pouvant détecter plus clairement la tendance de l'actif.
La moyenne mobile exponentielle, en pondérant plus les derniers prix, est plus sensible aux changements de tendance, anticipant la moyenne mobile simple et la moyenne mobile pondérée.
Moyenne mobile pondérée
La moyenne mobile pondérée tente d'attribuer une importance progressive aux prix les plus récents par rapport aux prix les plus anciens qui sont calculés. L'objectif est de lisser la série de prix, tout comme la moyenne mobile exponentielle, mais avec des pondérations différentes.
Cette moyenne est calculée en offrant une série de pondérations qui diminuent à mesure que le prix devient plus ancien, de sorte que le dernier prix sera le plus pondéré et le prix le plus ancien sera le moins pondéré. Les pondérations des données les plus récentes sont plus élevées que dans le cas de la moyenne mobile exponentielle.
Ainsi, un effet similaire à la moyenne mobile exponentielle est obtenu, car il permet de voir plus clairement la direction de sa tendance.
Stratégies avec des moyennes mobiles
Nous pouvons développer les stratégies suivantes avec des moyennes mobiles :
- Vous pouvez calculer des moyennes mobiles de différents périodes pour voir s'ils se croisent. Par exemple, si j'ai une moyenne à court terme de 25 jours et qu'elle traverse de bas en haut la moyenne mobile à long terme (imaginons 100 jours), nous sommes face à un signal d'achat. Si le sens de la croix était opposé, c'est-à-dire de haut en bas ou descendant, le signal serait de vente.
- Vous pouvez également concevoir des stratégies avec le graphique des prix et le graphique de sa moyenne mobile. Si le prix traverse à la hausse la moyenne mobile, c'est un signal d'achat. Par contre, si la croix est descendante, c'est un signal de vente.
- Vous pouvez utiliser trois moyennes mobiles. Celui qui inclut le plus de périodes sert de filtre, c'est-à-dire pour ouvrir une position d'achat (à la hausse), cette moyenne à long terme doit être inférieure aux deux autres. De même, pour ouvrir une position de vente (à la baisse), la moyenne à long terme doit être supérieure aux autres.
Voulez-vous en savoir plus sur d’autres indicateurs du trading ? Consultez notre article : Indicateurs de Trading.
Cas d'application des stratégies
Maintenant, voyons des cas où nous appliquons deux des stratégies expliquées : le croisement du prix sur la moyenne et le croisement des moyennes. Il convient de noter que les moyennes mobiles peuvent être optimisées pour calculer le nombre de séances qui est le mieux pour obtenir une plus grande rentabilité.
1. Le prix croise la moyenne mobile
(la ligne rouge est la moyenne mobile et la ligne noire est le prix)

Sur le graphique, nous pouvons voir un exemple de quelles opérations seraient effectuées dans le cas où l'on suivrait une stratégie de "prix croise la moyenne mobile simple de 20 périodes". En vert, nous observons les signaux d'achat et en rouge les signaux de vente ou d'ouverture de courtes. Nous pouvons constater que lorsque le marché est en tendance latérale, de nombreux signaux erronés sont offerts, mais lorsqu'il est en tendance claire, l'opération est réussie.
Il est important de souligner que, lorsque la moyenne mobile commence à perdre de la pente et à devenir plate, elle nous indique que la tendance est en train de s'épuiser.
2. Croisement des moyennes mobiles

Dans l'exemple, nous voyons le croisement d'une moyenne mobile exponentielle de 13 périodes (bleu) et une moyenne mobile de 70 périodes (rouge). Nous pouvons voir comment une stratégie à long terme peut bien fonctionner avec le croisement des moyennes, car elle évite de nombreux signaux erronés. La stratégie serait d'acheter lorsque la moyenne mobile bleue croise de bas en haut la moyenne mobile rouge, et de vendre lorsque la bleue croise en mode descendant la rouge.
3. Supports et résistances avec des moyennes mobiles
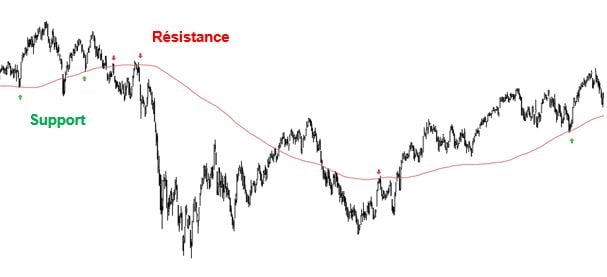
Sur le graphique, nous pouvons observer comment la moyenne mobile de 200 séances simple nous indique également certains supports (flèche verte) et résistances (flèche rouge).
Avantages et inconvénients des moyennes mobiles
Parmi les avantages des moyennes mobiles, nous pouvons citer :
- Ils sont relativement faciles à calculer (dans leurs trois types, il s'agit de moyennes).
- Ils permettent d'identifier des moments d'achat et de vente.
- Il permet à l'analyste de choisir le nombre d'observations à utiliser pour calculer la moyenne.
- Il permet de combiner différentes stratégies de trading.
Cependant, nous devons également observer quelques inconvénients :
- Ils montrent une tendance, mais pas son origine, nous ne savons pas pourquoi l'actif se déplace.
- Bien qu'il puisse être utile pour le trading à court terme, à plus long terme, l'investisseur pourrait être intéressé à analyser les fondements de l'actif, c'est-à-dire les variables qui influencent le mouvement de celui-ci. Dans ce sens, il recourra probablement à l'analyse fondamentale.
- C'est un indicateur retardé, c'est-à-dire qu'il montre le début ou le changement d'une tendance, mais ne permet pas de l'anticiper.
- Les moyennes mobiles sont de bons indicateurs de tendance, mais dans les tendances latérales (qui ne sont pas clairement haussières ou baissières) offrent une grande quantité de signaux erronés et contradictoires.
Exemple de moyenne mobile
Voyons un exemple simple en calculant les trois types de moyennes mobiles :
| Prix de l'action X | Moyenne mobile exponentielle | Moyenne mobile simple | Moyenne mobile pondérée | ||||
| 6,97 | |||||||
| 5,94 | |||||||
| 5,73 | |||||||
| 5,73 | |||||||
| 5,61 | 6,00 | 6,00 | 5,80 | ||||
| 5,61 | 5,87 | 5,72 | 5,67 | ||||
| 6,78 | 6,17 | 5,89 | 6,02 | ||||
| 5,21 | 5,85 | 5,79 | 5,79 | ||||
| 5,17 | 5,62 | 5,67 | 5,59 | ||||
| 5,22 | 5,49 | 5,60 | 5,44 | ||||
| 6,83 | 5,94 | 5,84 | 5,85 | ||||
| 5,96 | 5,94 | 5,68 | 5,89 | ||||
| 6,44 | 6,11 | 5,92 | 6,14 | ||||
| 5,13 | 5,78 | 5,92 | 5,88 | ||||
| 6,91 | 6,16 | 6,25 | 6,21 | ||||
| 6,24 | 6,19 | 6,14 | 6,20 | ||||
| 6,80 | 6,39 | 6,31 | 6,43 | ||||
| 5,06 | 5,95 | 6,03 | 6,01 | ||||
| 6,91 | 6,27 | 6,38 | 6,31 | ||||
| 5,06 | 5,87 | 6,01 | 5,86 |
| Prix de l'action X | Moyenne mobile exponentielle | Moyenne mobile simple | Moyenne mobile pondérée |
| 6,97 | |||
| 5,94 | |||
| 5,73 | |||
| 5,73 | |||
| 5,61 | 6,00 | 6,00 | 5,80 |
| 5,61 | 5,87 | 5,72 | 5,67 |
| 6,78 | 6,17 | 5,89 | 6,02 |
| 5,21 | 5,85 | 5,79 | 5,79 |
| 5,17 | 5,62 | 5,67 | 5,59 |
| 5,22 | 5,49 | 5,60 | 5,44 |
| 6,83 | 5,94 | 5,84 | 5,85 |
| 5,96 | 5,94 | 5,68 | 5,89 |
| 6,44 | 6,11 | 5,92 | 6,14 |
| 5,13 | 5,78 | 5,92 | 5,88 |
| 6,91 | 6,16 | 6,25 | 6,21 |
| 6,24 | 6,19 | 6,14 | 6,20 |
| 6,80 | 6,39 | 6,31 | 6,43 |
| 5,06 | 5,95 | 6,03 | 6,01 |
| 6,91 | 6,27 | 6,38 | 6,31 |
| 5,06 | 5,87 | 6,01 | 5,86 |
Nous avons donc des données sur le prix d'un actif pendant vingt périodes. Pour des raisons de praticité, nous allons calculer les moyennes mobiles en utilisant cinq périodes.
La moyenne mobile simple est une moyenne arithmétique, c'est-à-dire la somme des valeurs entre le nombre de données. Exemple :
moyenne de la période 5= (6,97+5,94+5,73+5,73+5,61)/5=5,996=6,00
De même, comme nous l'avons expliqué dans un autre article (moyenne mobile exponentielle), pour calculer l'EMA, nous utilisons comme première donnée la moyenne mobile simple. À partir de là, nous utilisons un facteur de lissage appelé k.
k=2/(1+p)=2/6=0,3333
*p est le nombre de périodes, c'est-à-dire 5 dans l'exemple.
Ensuite, nous recourons à la formule :
EMA de la période 6= prix de la période 6 * k + EMA de la période 5 * (1-k)
EMA de la période 6= 5,61*0,3333 +6*(1-0,3333)=5,87
Enfin, pour la moyenne mobile pondérée, chaque donnée est multipliée par un nombre entre 1 et 5, multipliant le période le plus éloigné par 1 et le plus proche par 5. Puis, divisez par 15 (la somme des nombres de 1 à 5).
Exemple :
(1*6,97+2*5,94+3*5,73+4*5,73+5*5,61)/15=5,80